Feedback mechanism in a rounded impinging jet: tonal vs broad-band noise
by
Rectorate/Building-Auditorium
GSSI
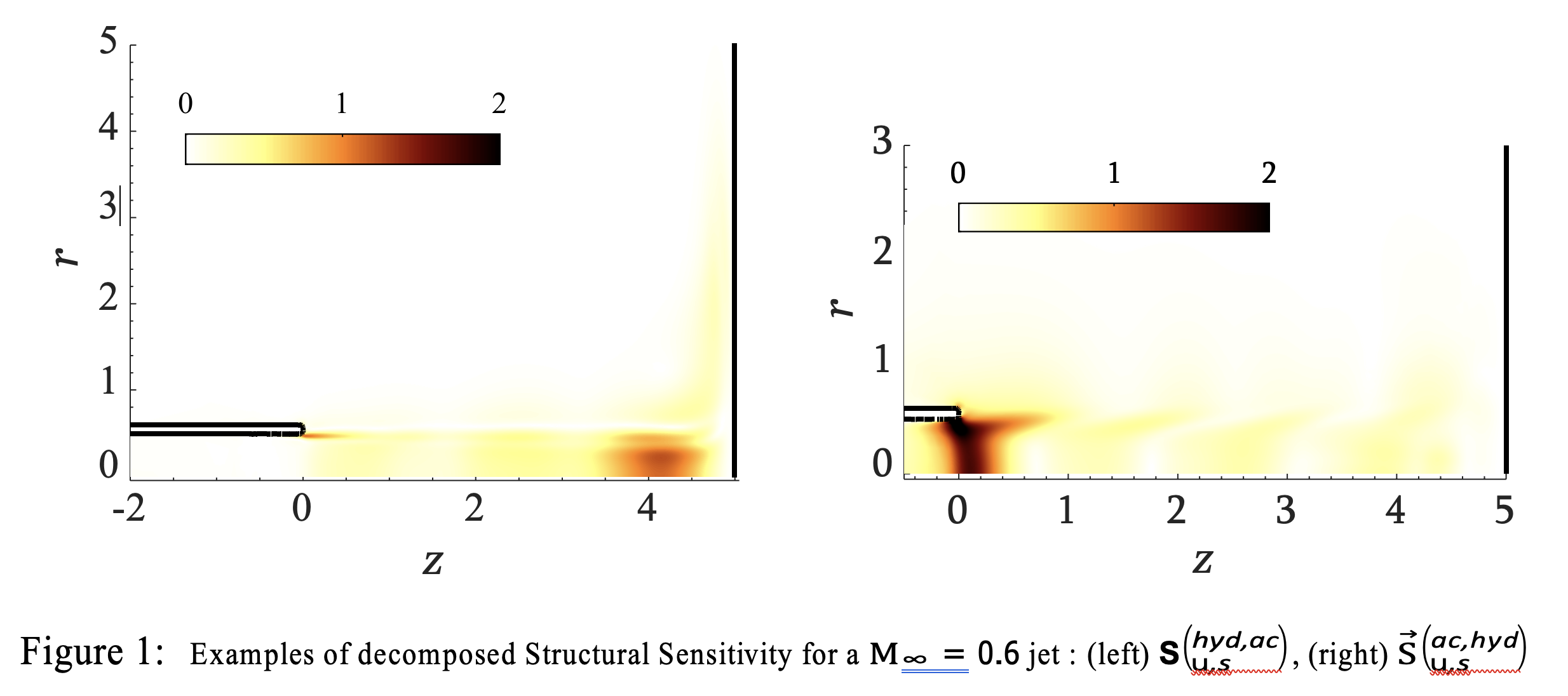
It is well known that impinging jets, under particular conditions, may radiate intense tonal noise [1]. In some cases, the sound generation isunderpinned by the presence of a self-excited instability originated by a feedback loop between two kind of waves: a downstream-travelling KH wave, which is excited at the nozzle lip and propagates around the jet core position, and an upstream-travelling wave generated by the impingement of disturbances on the plate and propagates backward inside/outside the jet core. The non-local constructive interaction of such wavesgives rise to a series of self-sustained global in time instabilities whose interactions, in some circumstances, are able to radiate an intense tonalacoustic field. In the presentation we will review the characteristics of the self-sustained mechanism and its noise radiation by using both a globaland a local stability analysis that will precisely identify the components of the feedback loop. In order to better understand the fundamental physical mechanism leading to tonal (or broadband) sound emission, we propose a novel acoustic-hydrodynamic decomposition of the structural sensitivitytensor (originally developed for spatially localized instabilities) [2], which serves to precisely localize the active regions of the long-range feedback loop (i.e. where the conversion between the two kind of waves takes place) and which is also suited to study other kind of long-range instabilitiessuch as thermo-acoustic, hydro-acoustic or thermo-diffusive instabilities. As an example, figures below show the results obtained by the proposed decomposition for a high subsonic case. Motivated by the results of such analysis, we then propose a minimal reduced model that faithfully represents the fundamental properties of the sound emission. More precisely, by applying equivariant bifurcation theory [3], we derive a reducedorder model based on a resonant interaction of a series of unstable Hopf bifurcations which qualitatively predicts the characteristics of the sound emission. Possible applications to other problems (cavity flow, flow through apertures and flow past airfoils) and extension to turbulent regime willbe briefly discussed.
[1] Tam , C. K. W. and Ahuja, K. K. (1990). Theoretical model of discrete tone generation by impinging jets. Journal of Fluid Mechanics, 214,67-87.
[2] Giannetti, Flavio, and P. Luchini (2007). Structural sensitivity of the first instability of the cylinder wake. Journal of Fluid Mechanics, 581,167-197.
[3] Moehlis, J. and Knobloch, E. (2007). Equivariant bifurcation theory, Scholarpedia, 2, 9, page 2511,
Francesco Viola
